第 1 頁 (共 1 頁)
請問兩題機率
發表於 : 2013年 9月 27日, 13:50
由 icebar
1.某年的校際盃桌球賽共有11所大學報名,A校和B校是其中的兩校。每所學校的實力均等,該年的賽程表如附圖。在每個學校都還沒有抽籤的情形下,則冠亞軍決賽時是A校和B校對決的機率是多少?
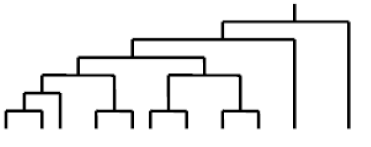
- game.png (4.3 KiB) 已瀏覽 12413 次
2.當投擲n個公正骰子一次,點數和為2008的機率與點數和為S的機率相等,則S的最小值為何?
Re: 請問兩題機率
發表於 : 2013年 9月 27日, 15:49
由 thepiano
Re: 請問兩題機率
發表於 : 2013年 9月 29日, 14:29
由 icebar
1.看了答案才知道可能是這樣想:
任意相異兩校對決的機會是一樣的,任取相異兩校有C(11,2)種,因此所求機率為1/C(11,2)。
不過,如果按照這樣的表去排,到底可以排出多少種賽程表呢?
2.看了連結的提示,覺得應該是這樣做:
n個骰子的點數和最少是n,最多是6n。
因為對稱的緣故,所以2008+S=n+6n,其中S≧n。
2008=7n-S≦7n-n=6n,得n≧335。
故S=7n-2008≧7*335-2008=2345-2008=337。
答案是337嗎?
這兩題這樣做不知道對不對,請thepiano老師再指點一下。
Re: 請問兩題機率
發表於 : 2013年 9月 29日, 15:30
由 thepiano
"指點"倒是不敢,不過小弟的淺見如下:
第 1 題
由左至右有 11 個位置
其中第 3、10、11 是單線,而 1 和 2 同一組(甲組),4 和 5 一組(乙組),6 和 7 一組,8 和 9 一組,共 4 組,後 2 組無組別之分
先排單線部份有 P(11,3) 種排法
再排甲組部份有 C(8,2) 種排法
接著排乙組部份有 C(6,2) 種排法
最後排其餘 2 組,有 C(4,2)/2 種排法
故所求 = P(11,3) * C(8,2) * C(6,2) * C(4,2)/2
第 2 題
您的答案正確