第 1 頁 (共 2 頁)
103 大安高工
發表於 : 2014年 5月 6日, 00:01
由 thepiano
第一部份的參考答案請見 20140505.doc,隨意寫寫,有誤請指正
Re: 103 大安高工
發表於 : 2014年 5月 6日, 09:30
由 johncai
第一部份的第3題我算6
Re: 103 大安高工
發表於 : 2014年 5月 6日, 11:38
由 thepiano
johncai 寫:第一部份的第3題我算6
您是對的,小弟有個地方看錯,已更正
Re: 103 大安高工
發表於 : 2014年 5月 6日, 20:51
由 thepiano
第 10 題
請參考附件
Re: 103 大安高工
發表於 : 2014年 5月 7日, 10:39
由 thepiano
第 3 題
寫一下小弟的做法
不失一般性,設 CD > OD
令 CD = x,OD = 4/3 - x
x^2 + (4/3 - x)^2 = 1^2
CD = (4 + √2)/6,OD = (4 - √2)/6
△BFO 和 △DOC 相似
BF + FO = (OB/CD)(DO + OC) = [6/(4 + √2)][(4 - √2)/6 + 1] = 3 - √2
△AOE 和 △DOC 相似
OE + EA = (OA/OD)(OC + CD) = [6/(4 - √2)][1 + (4 + √2)/6] = 3 + √2
所求 = 6
Re: 103 大安高工
發表於 : 2014年 5月 7日, 11:07
由 jamesbondmartin
請問老師
4. 我列的式子如下,但只得到 (0,0,0) 一解,希望告知我那裏錯了。
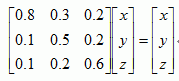
想請問 1. 2. 5.

Re: 103 大安高工
發表於 : 2014年 5月 7日, 11:31
由 thepiano
jamesbondmartin 寫:4. 我列的式子如下,但只得到 (0,0,0) 一解,希望告知我那裏錯了。
加上 x + y + z = 1
Re: 103 大安高工
發表於 : 2014年 5月 7日, 12:46
由 thepiano
第 1 題
x 分別用 1,-2,0 代入,可知 f(1) = f(-1) = f(0) = 0
f(x) = a(x - 1)(x + 1)x = a(x^3 - x)
唯一性的證明就留給您囉
第 2 題
bugmens 兄已有提示
http://math.pro/db/thread-1880-1-1.html
第 5 題
請參考附件
Re: 103 大安高工
發表於 : 2014年 5月 8日, 15:59
由 thepiano
填充第 2 題
請參考附件
Re: 103 大安高工
發表於 : 2014年 5月 17日, 18:13
由 LATEX
[quote="thepiano"]第 1 題
x 分別用 1,-2,0 代入,可知 f(1) = f(-1) = f(0) = 0
f(x) = a(x - 1)(x + 1)x = a(x^3 - x)
唯一性的證明就留給您囉
*****************
1.為什麼沒有 (x+2) 的因式 (用-2帶入), f(x)=ax(x-1)(x+1)(x-2)
2.可以寫一下唯一性的證明嗎?或者給一些題示?謝謝!